[Paper review] VAE - Auto-Encoding Variational Bayes (2013, ICLR)

남웅찬
Study/논문리뷰
2023. 5. 31.

이번에 리뷰할 논문은 VAE (Variational Auto-Encoder)로

잘 알려져있는 'Auto-Encoding Variational Bayes'이다.

현재 multimodel deep generative model, diffusion 등 generative model에 대한

연구가 활발히 이루어지고 있어서 개인적으로 너무나도 리뷰해보고 싶었다.

처음에는 무턱대고 diffusion을 리뷰할려고 했지만 Autoencoder, VAE에 대한

선행지식은 물론 개념에 사용되는 Cross-entropy, KL-Divergence,

Bayesian inference 등에 대한 정리가 안되있는 상태로

수식파티의 diffusion 논문을 보니 정말 포기할까 생각했다.

하지만 난 눈물을 자주 흘리진 않지.

diffusion 논문 리뷰하기에 앞서 Variational Autoencoder을

먼저 알아보고 수식파티에 적응해보기로 하였다.

'Auto-Encoding Variational Bayes' 논문 원문 링크는 아래와 같다.

https://arxiv.org/abs/1312.6114

Auto-Encoding Variational Bayes

How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets? We introduce a stochastic variational inference and learning

arxiv.org

Autoencoder

VAE를 이해하기 위해서 사전에 Information entropy, Cross entropy

그리고 KL divergence를 알아보았으니 본격적으로 VAE를 알아보기로 하자.

사실 뻥이다. 먼저 Autoencoder부터 알아보자.

~~(제가 지식이 많이 부족합니다.. 나대지 않고 차근차근 알아가보도록 하겠습니다...)~~

Autoencoder

VAE는 Variational Autoencoder의 약자로

2개의 파트로 나눠보자면 Variational 과 Autoencoder로 나뉘어진다.

Autoencoder가 무엇일까?

Autoencoder는 단순히 입력을 출력으로 복사하는 신경망이다.

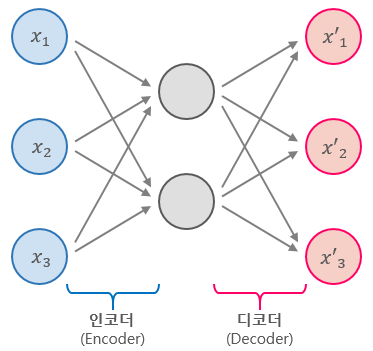
단순히 입력을 copy & paste 해서 복사하는 것이 아니라

중간에 hidden layer를 두고 여러가지 제약을 줌으로써

복사하려는 시도가 바로 autoencoder이다.

보통은 hidden layer의 뉴런 수를 input layer의 뉴런 수보다

작게 함으로써 데이터의 dimension을 축소한다던지

아니면 input으로 들어오는 값에 noise를 어느 정도 준 후

출력에서 noise를 제거하여 input을 복원하려는 시도들이

모두 autoencoder의 다양한 형태들이다.

이는 데이터를 효율적으로 representation하고자 고안된 방법이며

오히려 입력을 출력으로 바로 복사하려는 것을 방지함과 동시에

원본의 feature들을 잘 추출하려는 시도이다.

VAE (Variational Autoencoder)와 AE (Autoencoder) 두 가지 모두

representaion learning에 사용되는 neural architecture이나

몇 가지 차이점이 존재한다.

AE VS VAE

Autoencoder (AE)의 목적은 Encoder이다.

Input x를 효율적으로 reconstruct하기 위한 잠재변수(latent variable) $z$를 만드는 것,

또는 데이터를 저차원(latent space)으로 압축하는 과정에서 reconstruction error를

minimize하도록 학습하는 것이 autoencoder의 주된 목적이다.

그래서 사실 decoder는 학습하는 과정에서 필요시되기에 붙여진 것이며

중요한 것은 encoder인 것이다.

반대로 Variational AE (VAE)의 목적은 Decoder이다.

latent vector $z$를 통해 새로운 분포를 갖는 데이터를 generate하는데 초점을 두며

가령, 생성해내려는 확률 분포가 가우시안 분포라면

latent vector를 토대로 원본 데이터 분포와 유사한 특정 $\mu$와 $\sigma$일 때의

가우시안 분포를 찾으려는 시도이다.

그래서 VAE는 latent vector $z$의 확률적 표현에 집중하기 때문에

generative model에 해당하며 AE는 generative model이 아닌

compression and reconstruction model에 해당한다.

다르게 표현해보면 AE는 latent vector $z$를 결정하고자 하는

discriminative model일 것이고 VAE는 stochastic model이라고 할 수 있을 것 같다.

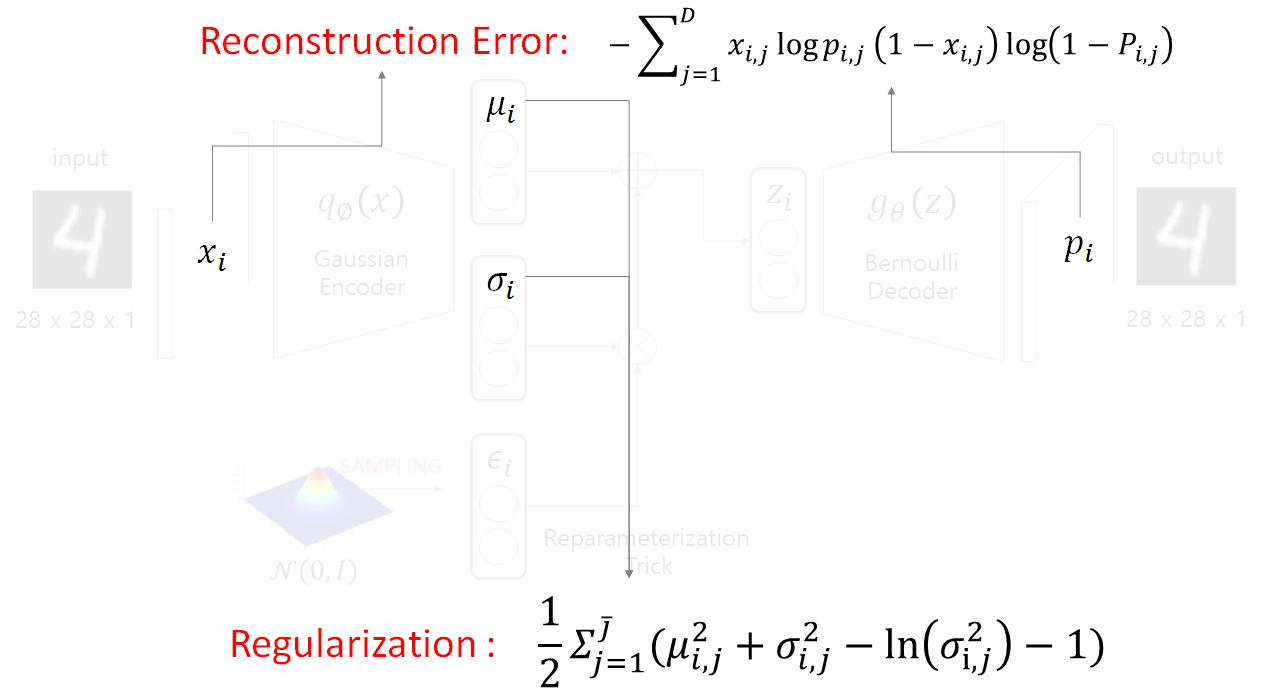
VAE Architecture

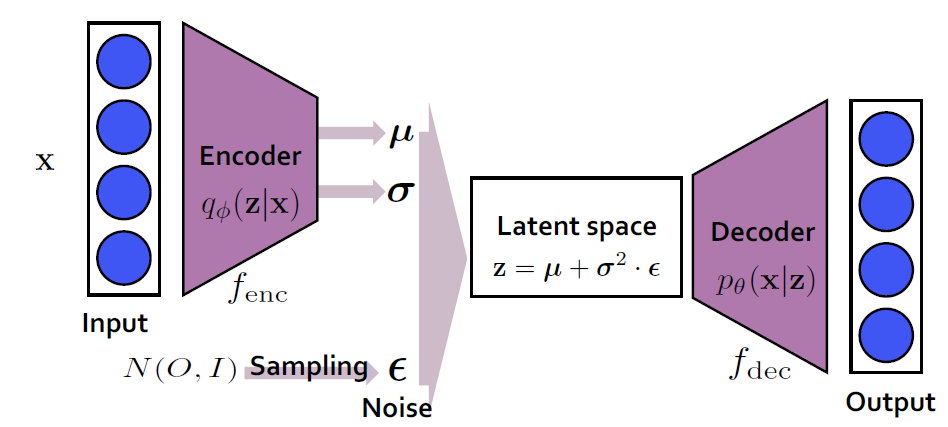
VAE의 architecture는 위의 그림과 같다.

입력 데이터로 들어온 이미지 input x가 주어졌을 때

먼저 encoder에 통과하여 input x 를 잘 나타낼 수 있는

latent vector $z$의 분포를 찾고자한다.

이 때, encoder 부분에서는 feature는 가우시안 분포를 따른다고

가정하기 때문에 결과적으로 input x와 가장 유사한

가우시안 분포가 무엇인지, 그 가우시안 분포가 $\mu$, $\sigma$ 일 때를

parameter로 두어 이를 찾게 된다.

Reparameterization trick

위의 architecture를 보면 $\mu$와 $\sigma$를

토대로 latent vector $z$를 바로 sampling하지 않고

표준 정규분포 $N(O, I)$에서 $\epsilon$을 sampling한 후

$ z = \mu + \sigma * \epsilon$ 하는 식으로 latent vector $z$를 정의한다.

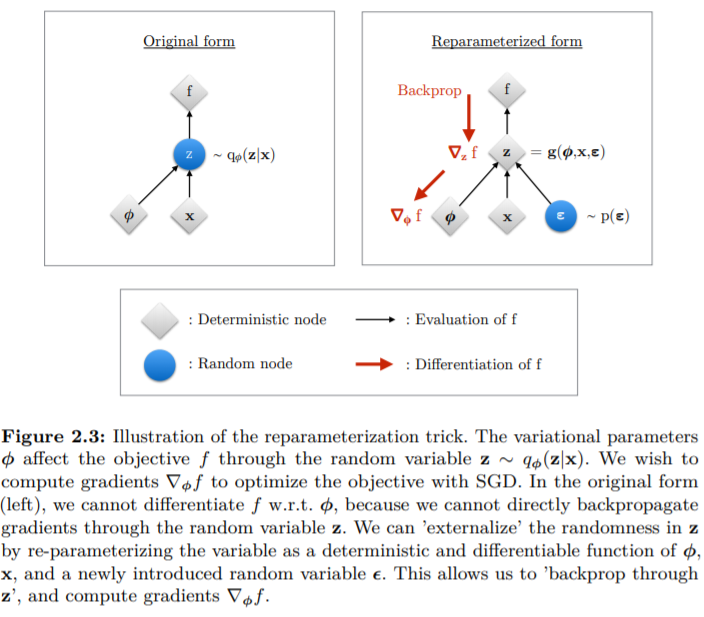
VAE에서는 latent vector를 굳이 $\mu$와 $\sigma$만을 사용하지 않고

별도의 표준 정규분포에서 $\epsilon$을 sampling하여

$ z = \mu + \sigma * \epsilon$ 하는 방식으로 $z$를 정의하는데

이러한 것을 reparameterization trick이라고 한다.

직역해보면 '재표현 장난'이라고도 해석할 수 있는데

이 reparameterization trick을 하는 이유로는 크게 2가지로 설명한다.

첫번째로는 다양한 output을 생성해내기 위함이다.

만약 $\epsilon$을 sampling하지 않는다면 동일한 input x마다

똑같은 $\mu$, $\sigma$가 산출될 것이고

이를 decoder input으로 넣으면

매번 동일한 output을 얻기 때문에 사실 autoencoder와 별반 다른게 없어진다.

VAE는 generative model로 input x에 대해 input x의 분포를 잘 이해하고

이에 따라 다양한 이미지를 생성해내는 것에 목적을 두기 때문에

랜덤하게 sampling을 함으로써 매번 조금씩 다른 output을

만들어내기 위해 표준 정규분포에서 sampling을 진행한다.

두번째로는 backpropagation을 위함이다.

Encoder를 통해 나온 $\mu$와 $\sigma$ 모두

사실상 $q_\phi (z|x)$의 모수인데

이 모수를 바탕으로 가우시안 분포로부터

바로 decoder에서 sampling할 경우 미분이 불가능해진다.

그래서 latent vector $z$를 $\mu$ + $\sigma$ * $\epsilon$ 식의

곱셈 및 덥셈으로 표현하게되면 chain rule이 끊기지 않고

backpropagation이 가능해져 학습이 비로소 가능해진다.

ELBO (Evidence Lower BOund)

정리해보면 encoder는 reparameterization trick을 기반으로

latent vector $z$를 찾는 것이고

decoder는 latent vector $z$를 기반으로

$p_\theta(x|z)$ 즉, input x가 나올 확률이 제일 높은

확률 분포를 추정하게된다.

우선 input x라는 데이터가 주어져있을 때

나올 확률이 제일 높은 확률 분포를

추정한다는 말의 의미를 알아보기로한다.

한국말로는 최대우도법(Maximum Likelihood Estimation, 이하 MLE)이라

알려져 있는 MLE가 바로 위의 말과 동일하게

데이터가 주어져있을 때 그 데이터가 나올 확률이 제일 높은

확률 분포를 추정하는 방법론이다.

MLE는 VAE의 근간이 되는 방법이기에

간단하고 빠르게 알아보기로 한다.

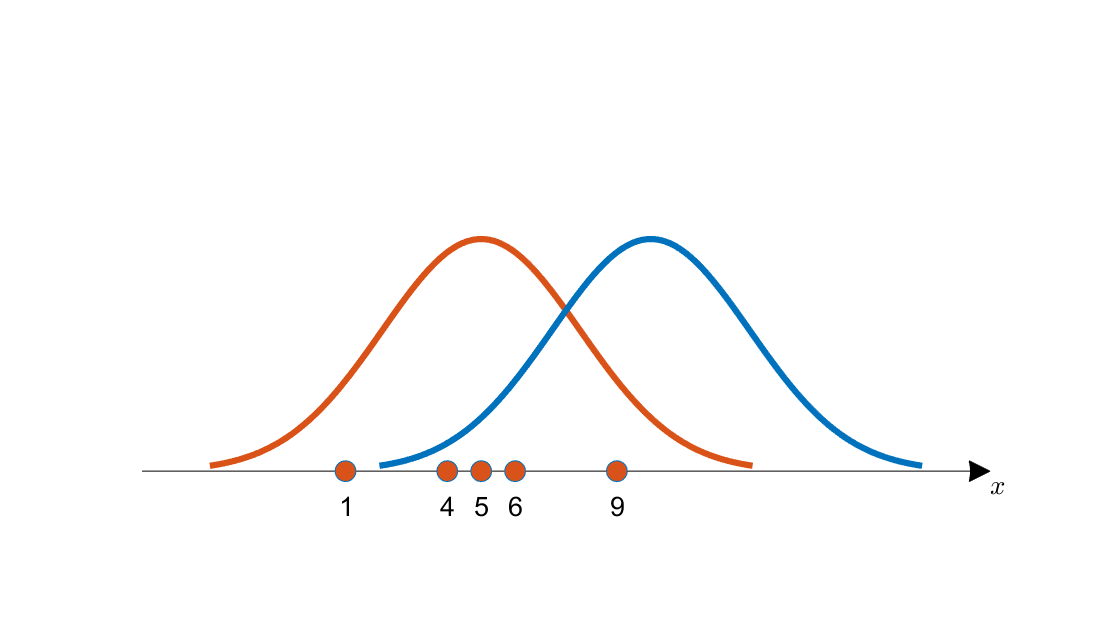
만약 위의 그림과 같이 x = {1, 4, 5, 6, 9}가 주어졌을 때

빨간색 분포와 파란색 분포 중 어떤 분포에서

x가 추출될 확률이 더 높은지 추정하는 방식이다.

정리하자면, 우리는 여러 픽셀들의 값으로 이루어져있는 input x의 값을

MLE 방법을 통해 어떤 특정 확률 분포에서 나올 확률이 제일 높은지

추정한 후 결정된 특정 확률 분포로부터 random하게 sampling한 후

input x와 비교를 해본 후 가장 유사할 때의 sampling된 데이터가

우리가 generate한 output이 되는 것이다.

그렇다면 우리는 먼저

input x가 등장할 확률이 제일 높은 확률 분포를

MLE 방식으로 찾아내야한다.

즉, log를 붙여 $\log p_\theta(x)$를 maximize하는 방식으로

loss function을 정의하게된다.

자. 이제 전개해나가보자.

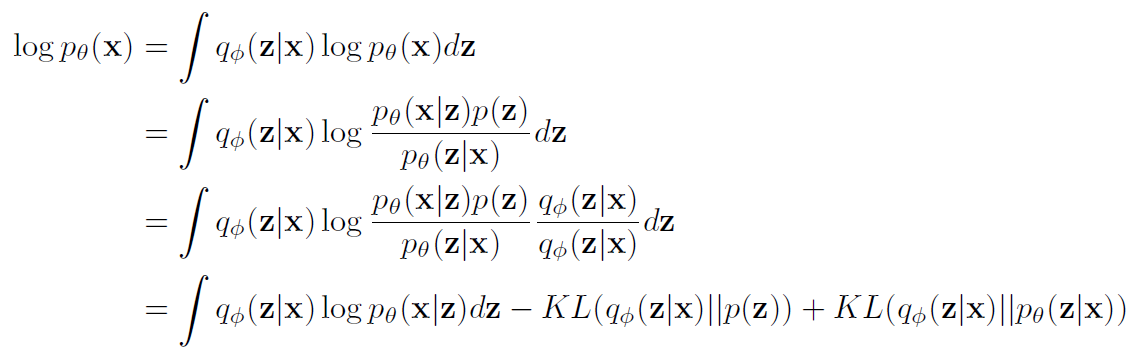
전체 전개식은 위와 같은데

차~근~차~근 해나가보기로 한다.

할 수 있다. 뭐 까짓거.

(할 수 있다를 계속 외치면 할 수 있다고 누가 그랬다.

할수있다할수있다할수있다하기싫어할수있다할수있다

할수있다할수있다할수있다할수있다할수있다할수있다)

STEP1.

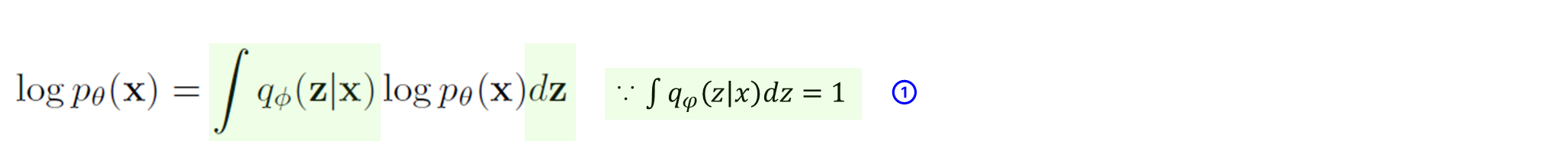
처음에 $\log p_\theta(x)$에 $\int q_\phi(z|x)dz$가 곱해졌는데

이는 모든 sample $x_i$에 대해 샘플 $z$가 생성될

확률 밀도함수의 적분이기 때문에 1이 되어버린다($\int q_\phi(z|x)dz = 1$).

어차피 1이기 때문에 계산가능한 식으로 전개하기 위해

곱해졌다고 보면 편할 것 같다.

STEP2.

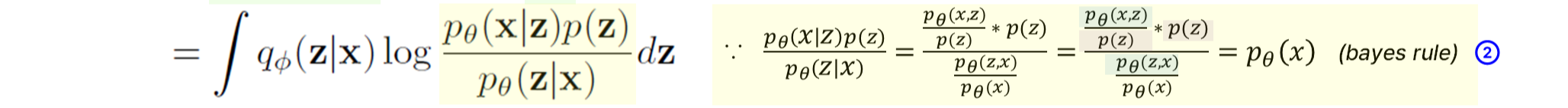
bayes rule을 적용하여 $p_\theta(x)$를 $\frac{p_\theta(x|z)p(z)}{p_\theta(z|x)}$로 변환한다.

증명은 옆에 살포시 적어놓았다.

STEP3.

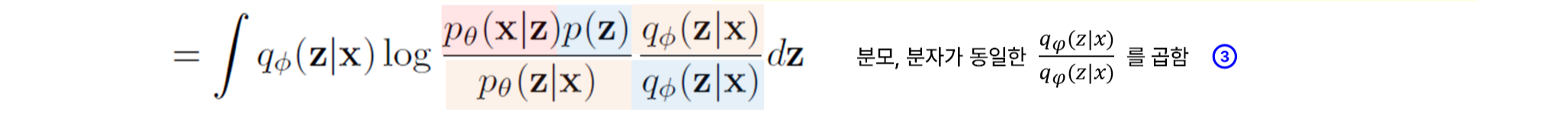
그 다음으로 분모, 분자가 동일한 $\frac{q_\phi(z|x)}{q_\phi(z|x)}$를 곱해주는데

나중에 KL-divergence로 표현하기 위해 곱해주는 것 같다.

STEP4.

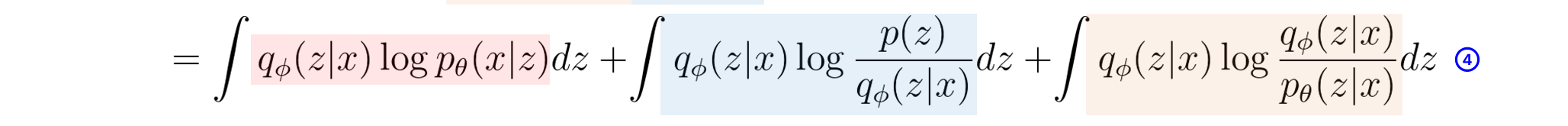
STEP4는 원래 maximum likelihood를 전개해나가는 과정에서

당연해서 생략이 되어있지만 직관적으로 이해되지 않아

직접 추가해보았다. ~~(자세히 보면 z랑 x의 필기체가 다릅니다. 감쪽같죠. 죄송합니다.)~~

STEP3에 있던 것을 log의 성질에 따라 3개의 항으로 정리한 것 뿐이다.

STEP5.

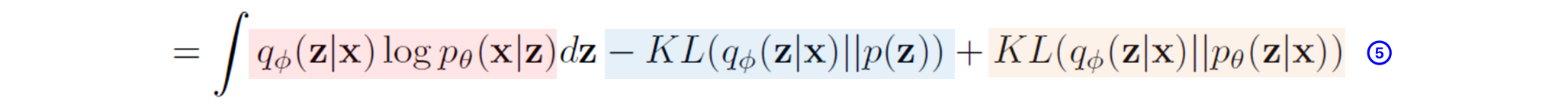
다 끝났다. STEP4에 있던 것을 첫 번째 항은 그대로 냅둔 후

두 번째 항과 세 번째 항을 초기에 알아보았던 KL-divergence로 나타낸 것이다.

$KL(P||Q) = \int P(x)\log_b\left(\frac{P(x)}{Q(x)}\right)$

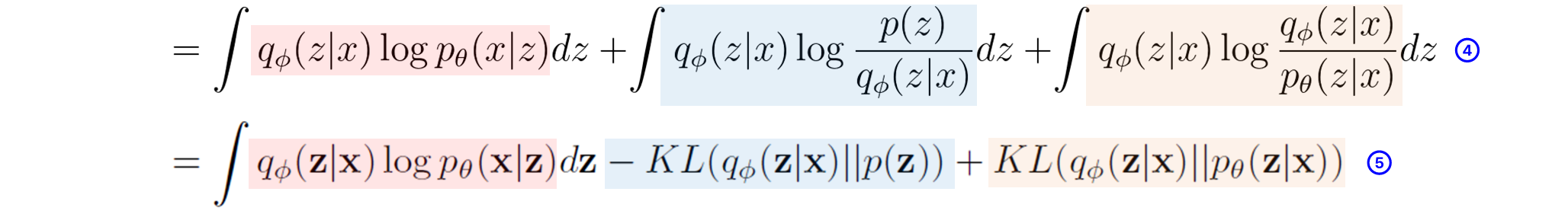
여기서, 세 번째 항은 그대로 양수로 오지만

두 번째 항은 분모&분자의 위치가 양수인 KL의 공식과 반대이다.

하지만, 단순히 역수를 취하게 되면 부호가 마이너스인 KL-divergence로 표현이 가능해진다.

$KL(P||Q) = \int P(x)\log_b(\frac{P(x)}{Q(x)}) = - \int P(x)\log_b(\frac{Q(x)}{P(x)})$

Evidence lower bound

우리는 여태까지 loss function을 선택하기 위해

$logp_\theta$를 maximize하려는 MLE 방식으로 알아보았다.

그래서 위의 식과 같이 정리 및 전개함으로써

3개의 항으로 이루어진 loss function을 얻을 수 있었다.

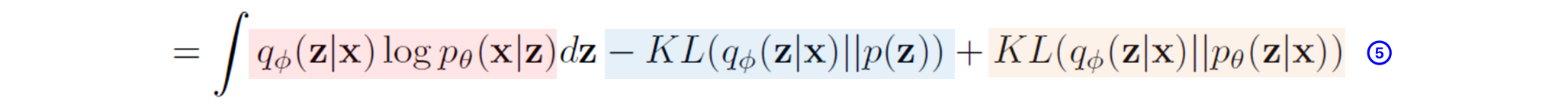
여기서 옥의 티가 있는데 찾았다면 정말 천재이신거다.

옥의 티는 바로 세 번째 항에 있는 $p_\theta(z|x)$이다.

encoder 부분의 과정은 $q_\phi(z|x)$이고

decoder 부분의 과정은 $p_\theta(x|z)$인데

$p_\theta(x|z)$의 반대과정인 $p_\theta(z|x)$는 알 수가 없다.

하지만, KL-divergence는 무조건 0 이상인 non-negative의 성질을 지니는데

이를 Jensen's Inequality로 증명하면 non-negative임을 알 수 있다.

이는 아래의 글에 정말 친절하게 나타내주셨다.

https://hyunw.kim/blog/2017/10/27/KL_divergence.html

초보를 위한 정보이론 안내서 - KL divergence 쉽게 보기

사실 KL divergence는 전혀 낯선 개념이 아니라 우리가 알고 있는 내용에 이미 들어있는 개념입니다. 두 확률분포 간의 차이를 나타내는 개념인 KL divergence가 어디서 나온 것인지 먼저 파악하고, 이

hyunw.kim

직관적으로 이해하고자 한다면

KL-divergence는 두 확률분포가 얼마나 차이가 나는지를 나타내는 지표이기 때문에

$KL(P||Q)$는 확률분포 P가 Q와 동일할 때 최솟값 0을 가진다.

그래서 KL-divergence가 non-negative하다는 성질을 이용하여

$p_\theta(z|x)$는 모르지만 무조건 0보다 크다는 것을 알기 때문에

목적함수 즉, loss function의 하한 경계를 다음과 같이 표현할 수 있다.

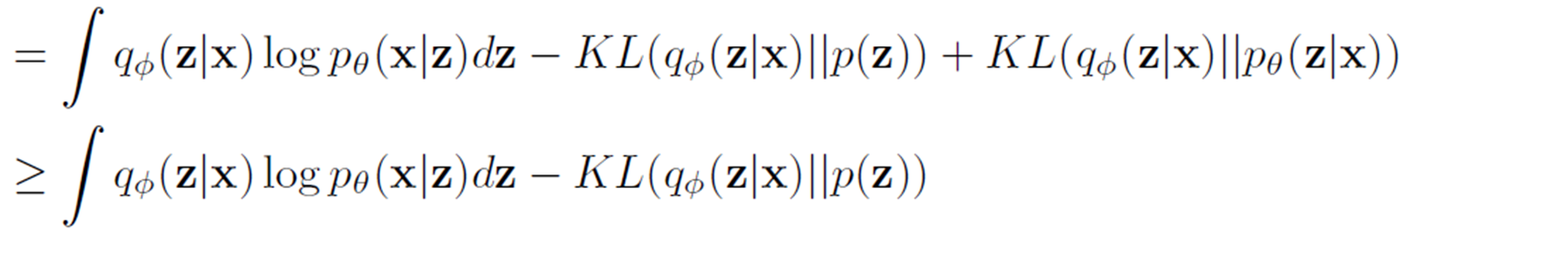
여기서 본래 목적이었던

$\log p_\theta(x)$를 maximize하는 것을

$q_\phi(z|x)\log p_\theta(x|z)dz - KL(q_\phi(z|x)||p(z))$를 maximize하는 것으로

목적함수를 변경함으로써 학습을 진행한다.

$q_\phi(z|x)\log p_\theta(x|z)dz - KL(q_\phi(z|x)||p(z))$ 이 부분을

바로 Evidence Lower Bound 줄여서 ELBO라고 하며

ELBO를 maximize하는 것으로 학습을 진행하는 것이

VAE의 핵심이다.

ELBO = Reconstruction error + Regularization error

여기서, 앞의 항을 Reconstruction error라고 하며

뒤의 항을 Regularization error라고 하는데

이름의 의미를 곱씹으면 바로 이해가 가능해진다.

VAE는 크게 2가지의 목표를 가지고 학습이 진행되어진다.

1. latent vector $z$를 토대로 input x와 유사하게 generate

2. input x와 유사한 latent vector $z$를 estimate

즉, 우선 VAE는 generative model이기 때문에 최대한

input x와 유사한 data를 generate해야하기 때문에

latent vector $z$를 토대로 reconstruction을 잘 해야하며

latent vector $z$를 토대로 reconstruction을 잘 해내긴 위해서

좋은 quality 즉, input x를 잘 나타내는 latent vector $z$를 estimate해야한다.

Reconstruction error를 기댓값의 형태로 바꿔서 재표현하면

$E_{q_{\phi(z|x)}}[\log p_\theta(x|z)] - KL(q_\phi(z|x)||p(z))$로 나타낼 수 있는데

이를 maximize하기 위해선 prior로 latent vector $z$가 주어졌을 때

posterior input x가 잘 등장할 수 있도록 기댓값 $\log p_\theta(x|z)$을 크게하는 것이고

input x와 latent vector $z$끼리 최대한 유사하도록

prior $p(z)$와 posterior $q_\phi(z|x)$ 간의 차이가 0에 가깝게 하여

minimize하는 것이 곧 ELBO를 maximize하는 것이다.

(별도) python code (ELBO 실제 계산하는 방법)

VAE encoder, decoder를 low-code로 직접 구현해보진 않았지만

실제로 python에서는 reconstruction error, regularization error를

어떻게 계산하는지 요 부분만 궁금하여 찾아보았다.

Reconstruction error 계산방법

Reconstruction error calculation using Monte-carlo tenchnique

Reconstruction error는 모든 $z$에 대해 적분을 진행해야하는데

요걸 실제로 어떻게 계산하는지, python code로는 어떻게 구현해야하는지

궁금증이 생겨서 별도로 정리해보았다.

모든 $z$에 대해 적분이 어렵기 때문에 VAE는

Monte-carlo simulation을 적용한다.

Monte-carlo simulation은 어떤 분포를 가정한 후

그 분포에서 무수히 많은 sampling을 진행한 후

그 평균이 곧 true 기댓값과 거의 동일해질 것이라는 가정이다.

근데 무수히 많은 sampling은 너무나 비효율적이기에

실제로는 sampling을 1번만 한다고 한다.

즉, L을 1로 둔 후 그 값을 대표값으로 사용한다고 한다.

그리고 위 글에서 놓친 부분이 바로

encoder q의 분포는 gaussian distribution을 가정하고

decoder p의 분포는 bernoulli distribution을 가정한다는 점을

넘어갔었다.

decoder p의 분포를 왜 bernoulli distribution으로 가정하는지

살짝 이해가 안됐었는데 개인적인 생각으로는

reconstruction error를 bernoulli distribution으로 가정함으로써

쉽게 계산이 가능해지기에 그러지 않았나 싶다.

(decoder p의 분포를 gaussian distribution으로 해도

결국 MSE로 계산할 수 있을 것 같다.)

어찌됐건 cross-entropy로 쉽게 표현이 가능해져

연산이 가능해진다.

Regularization error 계산방법

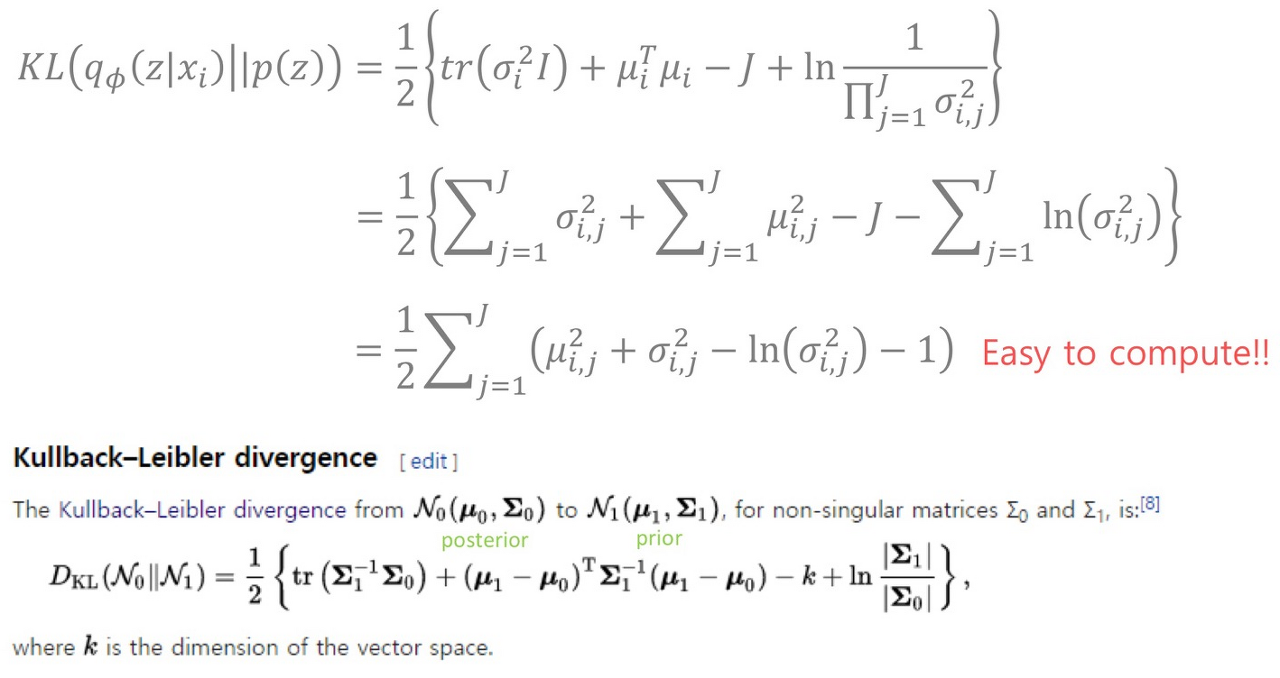
Regularization error calculation using Gaussian-distribution assumptions

Regularization error는 encoder를 거쳐서 나온 $q_\phi(z|x_i)$와 $p(z)$간

KL-divegence를 비교하는 것인데

앞서 encodeer p는 gaussian distribution을 가정하였고

latent vector $z$는 표준 정규분포를 가정한다고 한다.

그래서 latent vector $z$는 평균이 0, 표준편차가 1이기에

식이 1/2로 표현된 마지막 부분처럼 정리가 된다고 한다.

정리

python code

class VAE(keras.Model):
    def __init__(self, encoder, decoder, **kwargs):
        super().__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder
        self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
        self.reconstruction_loss_tracker = keras.metrics.Mean(
            name="reconstruction_loss"
        )
        self.kl_loss_tracker = keras.metrics.Mean(name="kl_loss")

    @property
    def metrics(self):
        return [
            self.total_loss_tracker,
            self.reconstruction_loss_tracker,
            self.kl_loss_tracker,
        ]

    def train_step(self, data):
        with tf.GradientTape() as tape:
            z_mean, z_log_var, z = self.encoder(data)
            reconstruction = self.decoder(z)
            reconstruction_loss = tf.reduce_mean(
                tf.reduce_sum(
                    keras.losses.binary_crossentropy(data, reconstruction), axis=(1, 2)
                ) # cross-entropy로 변환하여 reconstrunction error 계산
            )
            kl_loss = -0.5 * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var))
            # gaussian distribution을 가정하기에 위에서 본 공식대로 변환하여 계산
            kl_loss = tf.reduce_mean(tf.reduce_sum(kl_loss, axis=1))
            total_loss = reconstruction_loss + kl_loss # 단순히 reconstruction + kl 로 loss 정의
        grads = tape.gradient(total_loss, self.trainable_weights)
        self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
        self.total_loss_tracker.update_state(total_loss)
        self.reconstruction_loss_tracker.update_state(reconstruction_loss)
        self.kl_loss_tracker.update_state(kl_loss)
        return {
            "loss": self.total_loss_tracker.result(),
            "reconstruction_loss": self.reconstruction_loss_tracker.result(),
            "kl_loss": self.kl_loss_tracker.result(),
        }

마지막으로 keras에서 VAE class를 가져와보았다.

keras에서는 reconstruction error와 regularization error를

total_loss = reconstruction_loss + kl_loss로 합으로 계산하였고

부호는 반대로 해서 minimize하는 방식으로

loss function을 정의하는 것 같다.

여기까지 VAE를 알아보았다.

수식파티에 겁먹었지만

애플펜슬을 꼭 잡고

아이패드에 천천히 해보니까

은근 할만한 것 같았다.

다음은 diffusion이다.

기다리셈~

'Study > 논문리뷰' 카테고리의 다른 글

[Paper review] Transformer - Attention Is All You Need (2017, NIPS) (0)	2023.05.02
[Paper review] Resnet - Deep Residual Learning for Image Recognition (2015, CVPR) (2)	2023.04.24

Sidebar - Right

블로그 정보

남웅찬

ML/DL를 공부하는 야망가의 공부 정리 블로그

Follow Me

공지사항

검색

카테고리

분류 전체보기 (8)
- Study (8)
- Etc (0)

카테고리

분류 전체보기 (8)
- Study (8)
- Etc (0)

Woongardium leviosa