1장에서 Forward propagation을 알아보았다. 2장에서는 앞에서 진행했던 Foward propagation로만 model을 만들기엔 좋은 예측을 보장할 수 없기에 2장에서는 Forward propagation이 아닌 backward propagation과정과 더불어 weight를 Optimization하는 과정을 알아보고자 한다.
먼저 Weight에 따른 Error를 살펴보도록 하자.
다음과 같이 2개의 input과 weights 그리고 실제 값인 Actual value of Target이 13이라고 한 경우 Error는 9-13 = -4 가 된다.

-4라는 Error를 최소화하고 Model의 정확도를 높이고자 hidden layer에서 output으로 가는 weight를 수정해보자.
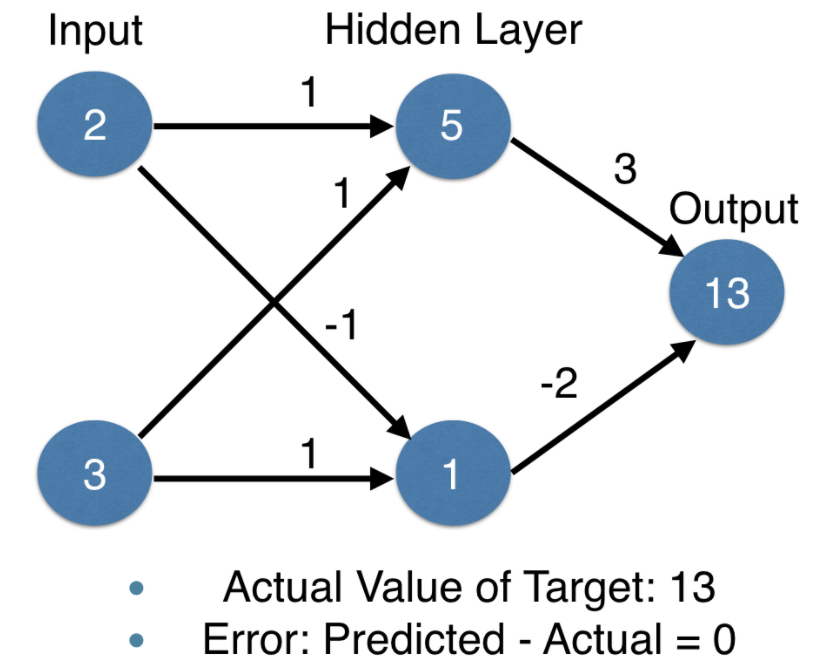
Weight를 수정한 경우 Predicted value가 13으로 Actual value of Target 과 동일하여 Error가 0이 된다. 이와 같이 weights에 따른 model의 정확도가 개선되는 것을 알 수 있지만 위의 예들은 Input이 2개 밖에 되지 않는 아주 simple한 neural network이다. 현실에는 너무나도 많은 data point가 존재하기에 data point가 많으면 많을수록 예측하기도 힘들 뿐더러 위의 예의 경우 한 개의 output을 위해서 weight를 Actual value of Target에 맞게 optimization을 진행할 수 있지만 모든 output에 적용할 수 있는 범용적 model을 설계할 시 각각의 data point 개수에 맞게 error가 발생한다.
아래의 코드는 weight list 중 특정 한 개의 값을 변경하여 오류 변화를 print 해본 것이다.
# Error calculation due to weight correction
input_data = np.array([0, 3])
weights_0 = {'node_0': [2, 1],
'node_1': [1, 2],
'output': [1, 1]
}
# The actual target value, used to calculate the error
target_actual = 3
# Make prediction using original weights
model_output_0 = predict_with_network(input_data, weights_0)
# Calculate error: error_0
error_0 = model_output_0 - target_actual
# Create weights that cause the network to make perfect prediction (3): weights_1
weights_1 = {'node_0': [2, 1],
'node_1': [1, 0],
'output': [1, 1]
}
# Make prediction using new weights: model_output_1
model_output_1 = predict_with_network(input_data, weights_1)
# Calculate error: error_1
error_1 = model_output_1 - target_actual
# Print error_0 and error_1
print(error_0)
print(error_1)아래의 코드는 단일 data point가 아닌 여러 개의 array로 구성된 list를 input으로 받았을 때 for문으로 iterate할 수 있도록 구현해 본 코드이다.
# Scaling up to multiple data points
from sklearn.metrics import mean_squared_error
model_output_0 = []
model_output_1 = []
for row in input_data:
model_output_0.append(predict_with_network(row, weights_0))
model_output_1.append(predict_with_network(row, weights_1))
# Calculate the mean squared error for model_output_0: mse_0
mse_0 = mean_squared_error(target_actuals, model_output_0)
# Calculate the mean squared error for model_output_1: mse_1
mse_1 = mean_squared_error(target_actuals, model_output_1)
# Print mse_0 and mse_1
print("Mean squared error with weights_0: %f" %mse_0)
print("Mean squared error with weights_1: %f" %mse_1)
print(weights_0)이러한 각각의 경우에 맞는 많은 개수의 Error를 통해 Model의 정확도를 판단하기엔 불가능하기에 사용하는 개념이 Loss fuction이다. Loss function(손실함수)은 오류를 모델의 예측 성능에 대한 단일 측정으로 통합한다. Model의 evaluation의 지표로 사용하는 것이 loss function이라고 보면된다. 일반적으로 회귀 모형에서 적용되는 MSE(Mean squared Error, 평균제곱오차)가 회귀 모형에서의 loss function인 것이다.
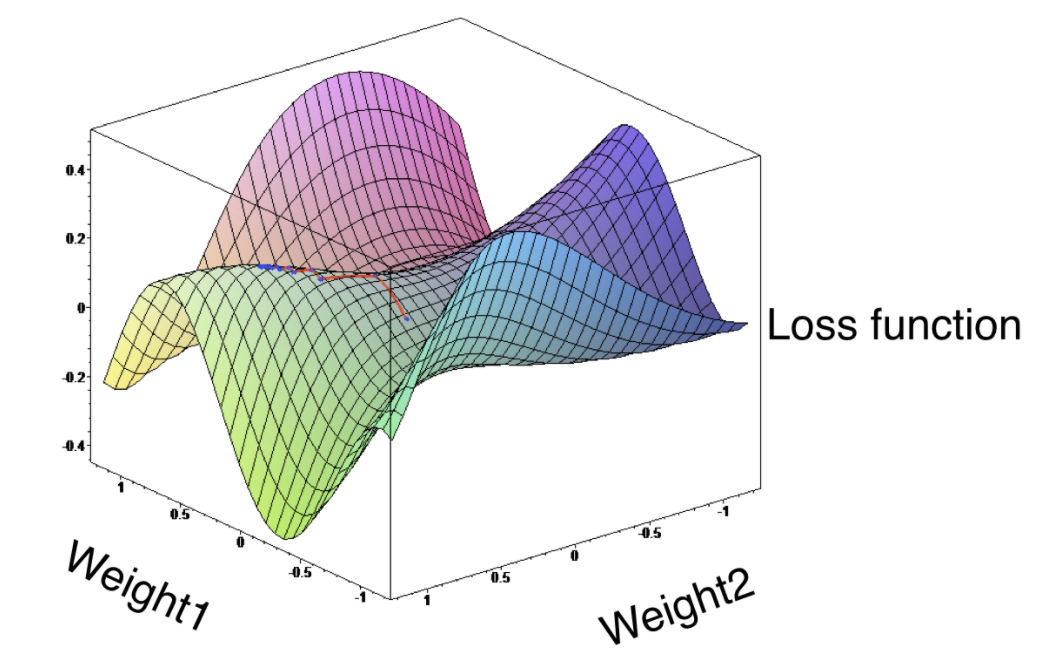
Loss function의 값은 낮으면 낮을수록 더 나은 모델을 의미하기 때문에 우리가 설계하고자하는 model의 목표는 loss function에 대해 가장 낮은 값을 제공하는 가중치 값을 찾는 것이다. 따라서 loss function이 어느 지점에서 가장 낮은 값을 제공하는지 탐색하는 과정이 필요시되는데 이 과정의 대표적인 방법이 Gradient Descent(경사하강법)이다.

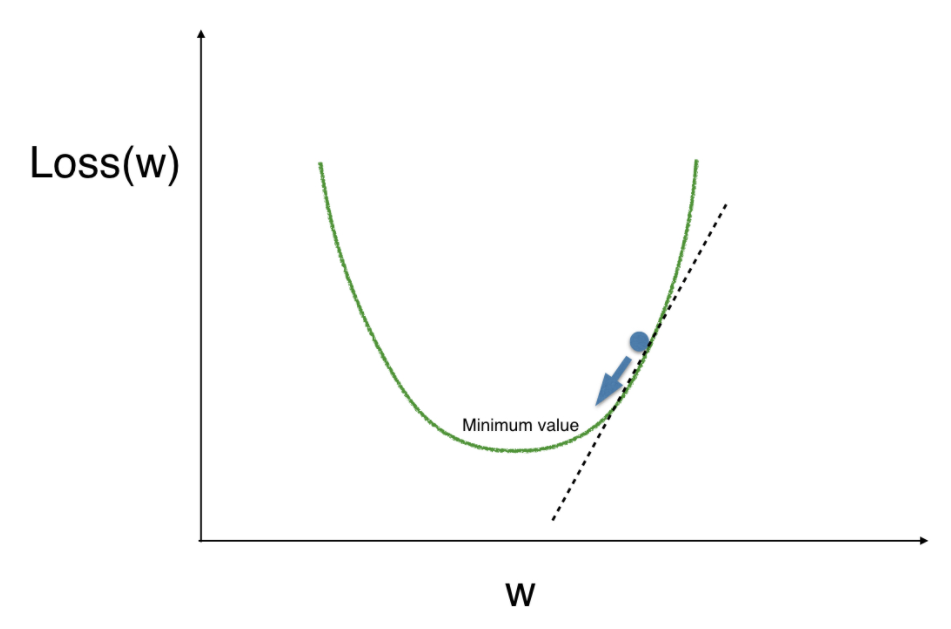
Gradient Descent 방식을 잘 이해할 수 있는 찰떡같은 비유가 바로 경사가 있는 곳에서의 암실이다. 우선 우리는 암실을 loss function이라고 한다면 가장 밑으로 가야한다는 목표를 가지고 있다. 위에서 말한듯이 Loss function의 값이 가장 낮을 때가 가장 높은 예측 정확도를 보이기 때문이다. 우리가 만약 이 암실에 어느 점에 위치해있다면 왼쪽이든 오른쪽이든 발을 한 번 디뎌보고 점점 경사가 완만해지는지 높아지는지 느끼면서 완만해지는 쪽으로 갈 것이다. 가다가 결국 점점 완만해지는 정도가 줄고 평지같은 느낌이 드는 특정한 점이 loss 값이 제일 낮은 minimum value인 것이다.
개인적인 궁금증이 생겨 찾아보았다. 보통 Gradient Descent 방식을 이해할 수 있도록 찾아볼 때 많이 찾아볼 수 있는 예는 loss function이 2차 함수의 형태일 때이다. 위에서 Gradient descent algorithm을 이해하기 위해서 설명된 시각화된 예도 loss function을 2차 함수로 가정하였다. 요기에서 궁금증이 생긴게 만약 loss function이 2차 함수가 아닌 3차 이상의 함수이면 어떨까?

위의 그림이 X축이 weight고 Y축이 loss function 이라고 가정해보자. Gradient descent 방식에 따르면 임의의 점에서 시작하여 극소점을 찾아가는 방식인데 loss function이 위와 같다면 노란색 local minima 인근 부분에서 시작했다면 local minima가 optimal weight이겠지만 빨간색 global minimum 인근 부분에서 시작했다면 global minima가 optimal weight가 된다. Gradient descent 방식에 의하면 임의의 점에서 시작하기에 local minima가 optimal weight가 될 수 있지만 명백히 global minima가 optimal weight이다.
신경망에서 이와 같은 문제가 흔히 발생하는데 Local minima는 부분적으로 봤을 때 극소점이 될 수 있는 점을 local minima(국소 최저치)라고 하며 전체적으로 봤을 때 극소점인 점은 global minima(전역 최저치)라고 한다. 이와 같은 문제를 막기 위해 train data에 random noise를 섞거나 반복적으로 계속 돌려가보면서 Global minima를 찾아낼 수 있도록 epochs, batch size, iteration 등을 조절하여 Optimal weight를 찾을 수 있도록 해야한다.
내 개인적인 궁금함은 그랬고.. 어쨌든 Gradient descent 방식을 통해 loss function이 제일 낮을 때를 탐색한다고하니 그럼 어떻게 찾아나갈까에 대해 알아보기로 한다. 왼쪽으로 갈지 오른쪽으로 갈지 어떻게 수학적으로 계산하는지 찾아보겠다는 말이다!
아주 간단한 예로 single data point에서 수정된 weight를 계산하는 예를 보자. 수정된 weight를 계산하기 위해서는 3개만 곱하면 된다. 첫 번째로 node의 값에 대한 loss function의 기울기 두 번째로 node의 값 그리고 세 번째로 activation function의 기울기이다.

두 번째와 세 번째부터 먼저 보면 node의 값은 주어진 값이고 activation function의 기울기의 경우 만약 ReLU가 activation function인 경우 x가 0보다 클 때 x의 값을 가지므로 기울기는 1이기에 두 번째와 세 번째는 주어지는 입력값과 설정한 activation function에 따라 쉽게 이해할 수 있었다.
자..이제 진짜 멍청했던 내 30분을 설명해보고자한다.. 내 멍청했던 30분은 첫 번째인 node의 값에 대한 loss function의 기울기이다.. 해당 예에서는 loss function으로 mean square error loss function을 사용한다고 가정했는데 mean square error loss function의 slope가 2*(predicted - actual) 이라고 슈슈슉 넘어가서 어 뭐지 하고 벙쪘다. MSE(mean square error)는 평균제곱오차로 loss function에 많이 쓰이고 나도 충분히 알고있던 개념이었는데 MSE의 기울기가 뭘까? 라고 생각해보니 벙찐 것이다. 우선 수학 특히 미적분학을 성실히 배우지 않았던 내 자신을 원망하며 그래도 30분 밖에 벙찌지 않은 나를 칭찬한다고 위로해야겠다.
어쨌든 고등학교 때 배운 f(x) = x^2 의 기울기는? 하면 2x라고 바로 나오는 주입식 교육을 기억하며 function의 slope를 구하기위해서는 function을 generalized formula로 나타내야하는 것이 중요하다. 그리고 또 중요한 것이 무엇을 변수로 놓고 표현할 것이다. x를 변수로 놓았기에 x에 대한 식으로 나타내는 것이 일반적으로 배워왔지만 무엇을 변수로 둘 지는 자유이며 그에 맞게 표현만 적절히 하면된다. ML/DL을 공부하면서 통계학과 선형대수 및 기초 수학에 대한 중요성을 이제서야 느낄 수 있었다. 쨌든! loss function으로 MSE를 선택한 경우 즉 오차에 대한 function으로 MSE를 채택한 경우 genaralized formula는 f(error) = (error)^2 이다. 즉, 그 때마다의 오차는 제곱오차를 채택한 것이며 model evaluation을 위해 이러한 제곱오차들에 대해 평균을 구하는 것이다. 그렇기에 MSE의 기울기는 2 * error 즉, 2 * (predicted - actual) 이다! 막상 내 머리 속으로 정리가 끝나니 별 것도 아닌 것 가지고 고민한게 부끄럽지만 그래도 내 머리로, 내 방식대로 정리되서 다행이다.
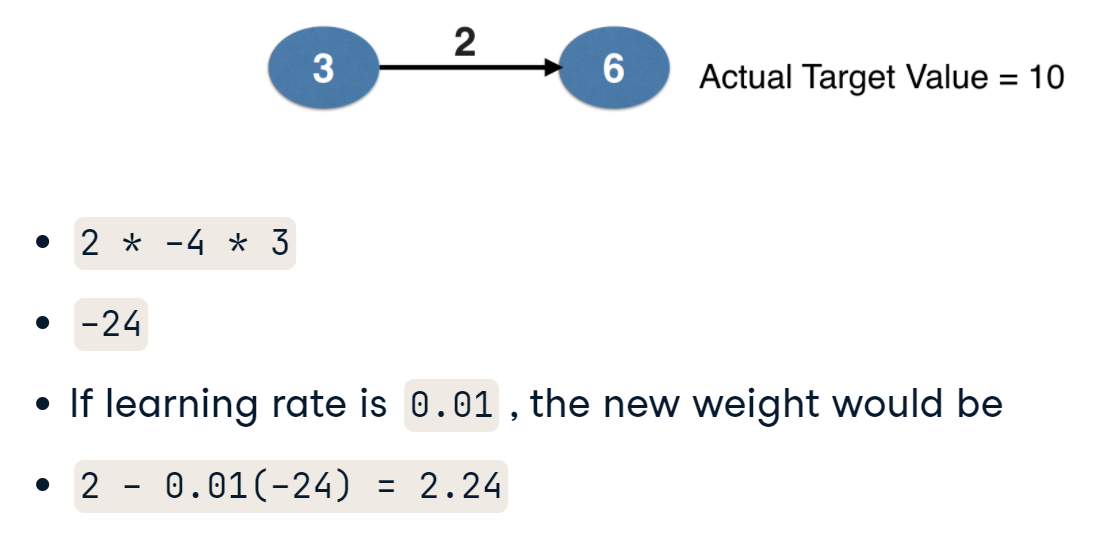
많이 돌아왔다.. 다시 updated weight를 구하는 것으로 돌아와서 updated weight를 구하는 방법은 위에서 말한 node 값에서의 loss function slop와 node value 그리고 activation function slope 이 모두를 곱해서 original weight에 substract 하면된다. 즉, original weight - loss function slope * node value * activation function slop 이고 이는 MSE를 loss function 으로 채택하고 activation function은 없다고 가정하였을 때 original weight - 2 * error * node value 이다.
대입해보자!
Updated weight = 2 - {2*(-4)*3} = 2+24 = 26이다. 여기서 보면 original weight가 2였으나 26으로 확 상승하였다. weight의 경우 계산에 의해 값이 많이 커질 수 밖에 없기에 size를 축소시키기 위해 사용하는 것이 바로 learning rate이다. 즉, 단계 크기를 결정하는 튜닝 매개변수로 사용되며 흔히 사용하는 값은 0.01이다. 이 learning rate를 아까 곱한 3가지에 곱해 weight를 update하면 된다. 그래서 최종 updated weight는 2 - (0.01)*{2*(-4)*3} = 2 + 0.24 = 2.24 이렇게 update 되는 방식이다.
아래 예는 multiple array 로 이루어진 input의 경우 updated weights 를 계산하는 코딩이다.
get_slope에는 2 * Error * input_data 가 계산되어지기에 weights = weights - slope * learning_rate만 하면된다.
# Making multiple updates to weights
n_updates = 20
mse_hist = []
# Iterate over the number of updates
for i in range(n_updates):
# Calculate the slope: slope
slope = get_slope(input_data, target, weights)
# Update the weights: weights
weights = weights - slope * 0.01
# Calculate mse with new weights: mse
mse = get_mse(input_data, target, weights)
# Append the mse to mse_hist
mse_hist.append(mse)
# Plot the mse history
plt.plot(mse_hist)
plt.xlabel('Iterations')
plt.ylabel('Mean Squared Error')
plt.show()여기까지 weight를 optimize 하는 과정을 알아보았다. 이제부터 더 복잡한 deep learning model들을 optimize 하기 위해 필요한 backpropagation에 대해 알아보고자 한다. 여태까지 진행해온 forward propagation은 hidden layer에서 output layer로 가는 순방향 전파였다. Backpropagation은 이와는 반대로 output layer에서 hidden layer 방향으로 향하는 방식이다.
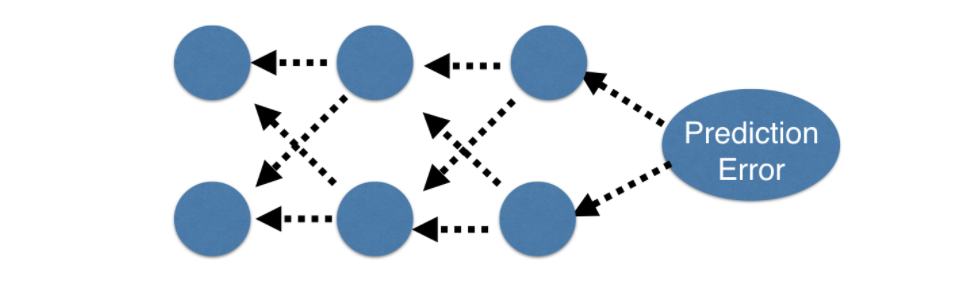
Backpropagation을 하기위해서는 실제 target 값과 predicted value 간의 error를 기반으로 weight를 update해야하기 때문에 forward propagation이 선행적으로 이루어져야한다. 즉, input layer로 부터 각 hidden layer를 지나치며 weight를 곱하고 activation function을 지난 다음 output layer에서 error를 계산하는 forward propagation을 진행한 후, 이제 update를 위해 순차적으로 back하며 propagation하는 방식이 Backpropagation다.
기본적인 방향이 역방향으로 진행되는 것을 알았으면 이제 어떻게 계산되는지 알아보기로 한다.
먼저 weight가 어떻게 update되는지를 알아보기로 한다. 위에서 말했듯이 updated weight를 위해서 곱해야하는 3가지 중에 slope of loss function이 필요했다. slope of loss function을 다른 말로 해보면 loss function을 weight로 미분한 값인데, 즉 loss function(error 값)을 작게 만들기 위해서 weight들이 loss function에 어느정도로 기여하고 있는지 그 방향성을 알기위해 slope(기울기)를 알아야한다는 말이다. 여기서 slope를 알기위해 필요한 개념이 Chain rule(연쇄법칙, 합성함수의 도함수)이다.
Chain rule은 아래의 식으로 표현될 수 있다.
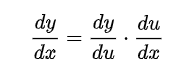
Chain rule은 간단하게 말하면 꼬리에 꼬리를 물며 겉함수에서 속함수를 곱하는 과정인데, 여러 개의 weight들과 bias들로 연산이 이루어진 loss function에서 특정한 한 개의 weight의 기여도 즉, slope를 알기위해 편미분한다는 것이다. 기여도(slope)를 알게 되었으면 이를 loss function을 줄일 수 있도록 gradient descent 방식으로 계속 update해나가면서 궁극적으로 target값과 가까워지도록 수정해나가는 것이 backpropagation인 것이다.
Chain rule에 대한 이해를 위해 직접 하나씩 해보며 잘 정리해주신 글이 있다.
(https://evan-moon.github.io/2018/07/19/deep-learning-backpropagation/)
보면서 정말 잘 이해가 되었습니다. 감사합니다..
여기까지 backprogation을 간략하게 알아보았다.
정리해보면 forward propagation을 진행한 후 predicted value와 target값의 차이 즉, loss function의 값을 줄이기 위해 weight를 update를 해야만 하였다. weight를 update하는 방식으로는 chain rule를 사용하여 weight가 loss function에 미치는 변화량 즉, slope(기울기)를 계산하여 이를 gradient descent 방식으로 조금씩 weight를 update하였다. 이 때, weight의 크기가 커지는 것을 방지하기 위해 적절한 learning rate를 설정하여 조금씩 수정해나가면서 global optima를 찾는 것이 backpropagation인 것을 알 수 있었다.

다음 글에서는 이제 3번째로 언급되었던 'Slope of the activation function'
즉, activation function(활성화 함수)에 대해 알아보고자 한다.
'Study > Deep learning tutorial' 카테고리의 다른 글
| [DataCamp] 3. Activation function (0) | 2023.04.24 |
|---|---|
| [DataCamp] 1. Basics of deep learning and neural networks (0) | 2022.03.04 |